2 Introduction to difference tests
2.1 Why Do We Compare Groups?
One of the goals of quantitative psychological research is the quest to understand differences: differences between individuals, groups, conditions, or time points. This pursuit is rooted in the scientific method, which relies on empirical evidence to support or refute hypotheses. When we compare groups in a study, we are essentially asking whether the differences we observe are meaningful or merely the result of random variation.
The underlying philosophy is that by systematically comparing groups, we can uncover patterns, relationships, and causal effects that contribute to our understanding of human behaviour, cognition, and emotions. These comparisons help us test theories, evaluate interventions, and make predictions about future outcomes. In essence, difference tests are the tools that allow us to determine whether observed variations are significant and worth further consideration, or if they can be attributed to chance.
To help clarify how we can compare groups in different research scenarios, let's explore the various statistical tests available, each suited to specific types of comparisons:
2.1.1 Comparing Two Groups: The T-Test
The t-test is one of the most commonly used statistical methods for comparing the means of two groups (i.e. an independent variable with two levels). It helps determine whether there is a significant difference between the two groups, considering the variability within each group.
Independent Samples T-Test: Used when comparing two independent groups (e.g., treatment vs. control).
Paired Samples T-Test: Used when comparing two related groups (e.g., pre-test vs. post-test scores for the same individuals).
2.1.2 Comparing Three or More Groups: One-Way ANOVA
When you have more than two groups to compare (i.e., an independent variable with more than two levels), a one-way Analysis of Variance (ANOVA) is used to determine whether there are statistically significant differences between the means of three or more independent groups. For example, if you were comparing the effectiveness of three different therapies on anxiety levels, a one-way ANOVA would be the appropriate test. We use ANOVA so that we can avoid performing multiple t-tests, which increases the risk of Type I errors (see chapter on power). ANOVA provides a single test that controls for this risk, offering a more reliable way to assess differences across multiple groups.
2.1.3 Comparing Multiple Factors: Factorial ANOVA
Factorial ANOVA extends the one-way ANOVA by allowing additional independent variables. This type of ANOVA not only examines the differences within independent variables, but also investigates possible interactions between independent variables.
For example, we could examine the effects of therapy type (CBT vs. psychotherapy) and session frequency (weekly vs. biweekly) on anxiety reduction. From performing a factorial ANOVA we can determine the main effect of therapy type, the main effect of frequency, and how the effectiveness of therapy type differs based on frequency (or vice versa).
2.1.4 Controlling for Covariates: ANCOVA
Analysis of Covariance (ANCOVA) combines ANOVA and regression. It allows for the comparison of group means while controlling for the influence of one or more continuous covariates. This helps in isolating the effect of the independent variable by accounting for variance that is explained by the covariates.
For example, Comparing the effectiveness of different teaching methods on exam performance while controlling for prior knowledge (measured by a pre-test score).
2.1.5 Extending to Multiple Dependent Variables: MANOVA
Multivariate Analysis of Variance (MANOVA) is used when there are multiple dependent variables, and it tests whether the mean differences among groups on a combination of dependent variables are significant.
For example, studying the effect of a training program on both job satisfaction and productivity simultaneously.
2.2 Choosing the appropriate test
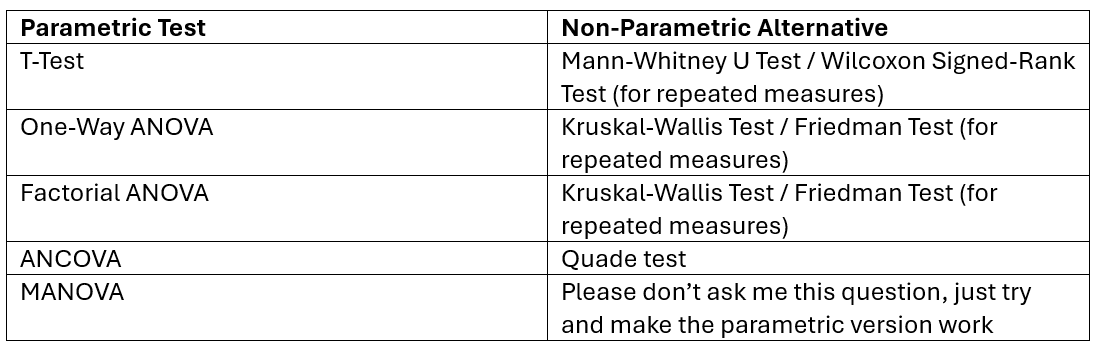
In this module, we will focus on ANOVA and factorial ANOVA, but it's also valuable to be aware of ANCOVA and MANOVA, especially if you consider using these techniques for your dissertation. Each of these tests is parametric, meaning they rely on certain statistical assumptions. Before using them, it is essential to conduct checks to ensure these assumptions are met. If the assumptions are violated, non-parametric alternatives should be used. While we will only cover the parametric tests in this module, the non-parametric alternatives are listed below for your reference in case you need to explore them for your dissertation.